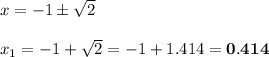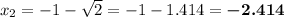Answer:
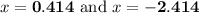
Explanation:
See attached graph for a visual
The x-intercepts of a graph are where the graph crosses the x-axis ie where the value of y = 0 The equation of the graph is y=-x^{2}-2x+1
Setting y = 0 and solving for the resultant equation will provide the x-intercepts
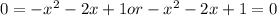
Reversing the signs gives us
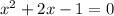
This is a quadratic equation of the form
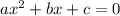 with a = 1, b = 2 and c=-1
with a = 1, b = 2 and c=-1
For an equation of this form the roots of the equation ie the values of x which satisfy the equation are given by
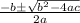
Substituting we get the two roots as

So the two roots are
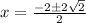
Dividing by 2 we get the two roots(x-intercepts) as