Question

Use the graph to write an equation of the line (90,9)

Answer 1

90-9=81

81+9=90

Explanation:

Answer 2

Equation tells us that for every 90 miles driven, the fuel in the tank decreases by 1 gallon, and the y-intercept is at 10 gallons, which is the amount of fuel when the distance is zero.

To write the equation of the line given in the graph, we need to follow these steps:

1. Identify two points on the line.

2. Calculate the slope
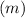`(\( m \))` of the line using the two points.

3. Use the slope and one of the points to write the equation in point-slope form.

4. Simplify the equation into slope-intercept form
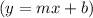`(\( y = mx + b \))`, if necessary.

Let's get started:

Step 1: Identify Two Points on the Line

From the graph, we have the point (90, 9) as provided. We need to identify another clear point on the line. By looking at the graph, it seems that the line crosses the y-axis at the point (0, 10).

Step 2: Calculate the Slope

The slope m of a line through points
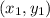`\( (x_1, y_1) \)` and
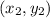`\( (x_2, y_2) \)` is given by:

`\[ m = (y_2 - y_1)/(x_2 - x_1) \]`

Using the points (90, 9) and (0, 10), we can calculate the slope as follows:

`\[ m = (10 - 9)/(0 - 90) = (1)/(-90) \]`

Step 3: Write the Equation in Point-Slope Form

The point-slope form of the equation of a line is:

`\[ y - y_1 = m(x - x_1) \]`

Using the point (90, 9) and the slope
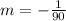`\( m = -(1)/(90) \)`, the equation is:

`\[ y - 9 = -(1)/(90)(x - 90) \]`

Step 4: Simplify into Slope-Intercept Form

Now we'll simplify the equation to get the y-intercept (b):

`\[ y - 9 = -(1)/(90)x + 1 \]`

`\[ y = -(1)/(90)x + 10 \]`

So, the answer is equation of the line in slope-intercept form is:

`\[ y = -(1)/(90)x + 10 \]`