**Disclaimer** Hi there! I assumed the purple triangle to be the one on the right. The following answer will be according to this understanding. If I am wrong, please let me know and I will modify my answer.
Answer:
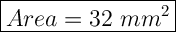
Explanation:
Given information
Rectangle A:
- Base (b) = 3 mm
- Height (h) = 9 mm
Rectangle B:
- Base (b) = 4 mm
- Height (h) = ?
Both rectangles have the same perimeter
Given formula
1) P = 2 (b + h)
- P = Perimeter
- b = base
- h = height
2) A = b × h
Find the height of rectangle B
Substitute values into 1) formula to find the perimeter of rectangle A
P = 2 (b + h)
P = 2 (3 + 9)
Simplify by addition
P = 2 × 12
Simplify by multiplication
P = 24 mm
Substitute values into 1) formula to find the perimeter of rectangle B
P = 2 (b + h)
24 = 2 (4 + h)
Divide 2 on both sides
24 / 2 = 2 (4 + h) / 2
12 = 4 + h
Subtract 4 on both sides
12 - 4 = 4 + h - 4
h = 8 mm
Find the area of rectangle B (Purple)
Substitute values into 2) formula
A = b × h
A = 4 × 8
Simplify by multiplication
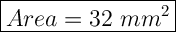
Hope this helps!! :)
Please let me know if you have any questions