I assume
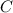 is oriented counterclockwise. If
is oriented counterclockwise. If
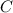 is the closed rectangle, then by Green's theorem we have
is the closed rectangle, then by Green's theorem we have
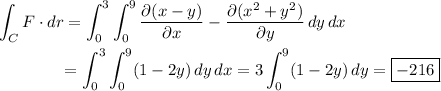
It seems unlikely, but if you actually are omitting the integral along the line segment joining (0, 9) and (0, 0), let
 and
and
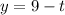 with
with
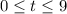 . Then the integral along this line segment would be
. Then the integral along this line segment would be

so that the overall integral would instead have -216 - 81/2 = -513/2.