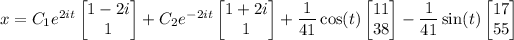Question

Use the method of undetermined coefficients to solve the given nonhomogeneous system. x' = −1 5 −1 1 x + sin(t) −2 cos(t)

Answer 1

It looks like the system is

`x' = \begin{bmatrix} -1 & 5 \\ -1 & 1 \end{bmatrix} x + \begin{bmatrix} \sin(t) \\ -2 \cos(t) \end{bmatrix}`

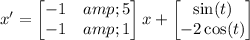
Compute the eigenvalues of the coefficient matrix.

`\begin{vmatrix} -1 - \lambda & 5 \\ -1 & 1 - \lambda \end{vmatrix} = \lambda^2 + 4 = 0 \implies \lambda = \pm2i`

For
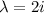`\lambda = 2i`, the corresponding eigenvector is
`\eta=\begin{bmatrix}\eta_1&\eta_2\end{bmatrix}^\top` such that

`\begin{bmatrix} -1 - 2i & 5 \\ -1 & 1 - 2i \end{bmatrix} \begin{bmatrix} \eta_1 \\ \eta_2 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix}`

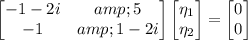
Notice that the first row is 1 + 2i times the second row, so

`(1+2i) \eta_1 - 5\eta_2 = 0`

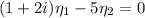
Let
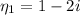`\eta_1 = 1-2i`; then
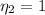`\eta_2=1`, so that

`\begin{bmatrix} -1 & 5 \\ -1 & 1 \end{bmatrix} \begin{bmatrix} 1 - 2i \\ 1 \end{bmatrix} = 2i \begin{bmatrix} 1 - 2i \\ 1 \end{bmatrix}`

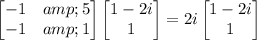
The eigenvector corresponding to
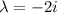`\lambda=-2i` is the complex conjugate of
`\eta`.

So, the characteristic solution to the homogeneous system is

`x = C_1 e^(2it) \begin{bmatrix} 1 - 2i \\ 1 \end{bmatrix} + C_2 e^(-2it) \begin{bmatrix} 1 + 2i \\ 1 \end{bmatrix}`

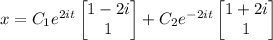
The characteristic solution contains
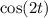`\cos(2t)` and
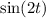`\sin(2t)`, both of which are linearly independent to
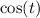`\cos(t)` and
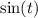`\sin(t)`. So for the nonhomogeneous part, we consider the ansatz particular solution

`x = \cos(t) \begin{bmatrix} a \\ b \end{bmatrix} + \sin(t) \begin{bmatrix} c \\ d \end{bmatrix}`

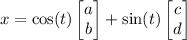
Differentiating this and substituting into the ODE system gives

`-\sin(t) \begin{bmatrix} a \\ b \end{bmatrix} + \cos(t) \begin{bmatrix} c \\ d \end{bmatrix} = \begin{bmatrix} -1 & 5 \\ -1 & 1 \end{bmatrix} \left(\cos(t) \begin{bmatrix} a \\ b \end{bmatrix} + \sin(t) \begin{bmatrix} c \\ d \end{bmatrix}\right) + \begin{bmatrix} \sin(t) \\ -2 \cos(t) \end{bmatrix}`

`\implies \begin{cases}a - 5c + d = 1 \\ b - c + d = 0 \\ 5a - b + c = 0 \\ a - b + d = -2 \end{cases} \implies a=(11)/(41), b=(38)/(41), c=-(17)/(41), d=-(55)/(41)`

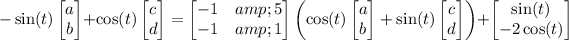
Then the general solution to the system is

`x = C_1 e^(2it) \begin{bmatrix} 1 - 2i \\ 1 \end{bmatrix} + C_2 e^(-2it) \begin{bmatrix} 1 + 2i \\ 1 \end{bmatrix} + \frac1{41} \cos(t) \begin{bmatrix} 11 \\ 38 \end{bmatrix} - \frac1{41} \sin(t) \begin{bmatrix} 17 \\ 55 \end{bmatrix}`