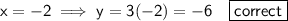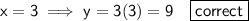2 Answers

Config · Answer 1 · 2023-11-13T02:55:08+0000

Answer:

? = 3

Explanation:

To find the value of ?, substitute one of the ordered pairs from the table [except (0, 0)] into the given formula and solve for ?.

Given formula:

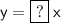
$\sf y=\boxed{?} \:x$

Substitute x = 1 and y = 3 into the formula:

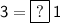
$\sf 3=\boxed{?} \:1$

To isolate ? divide both sides by 1:

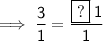
$\implies \sf (3)/(1)=\frac{\boxed{?} \:1}{1}$

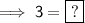
$\implies \sf 3=\boxed{?}$

Therefore, ? = 3:

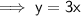
$\implies \sf y=3x$

Check by inputting another value of x from the table into the found formula and comparing the calculated y-value:

$\sf x=-2 \implies y=3(-2)=-6 \quad \boxed{\sf correct}$

$\sf x=3 \implies y=3(3)=9 \quad \boxed{\sf correct}$

Please log in or register to add a comment.