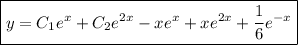Question

Use the method of undetermined coefficients to find the general solution to the de y′′−3y′ 2y=ex e2x e−x

Answer 1

I'll assume the ODE is

`y'' - 3y' + 2y = e^x + e^(2x) + e^(-x)`

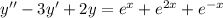
Solve the homogeneous ODE,

`y'' - 3y' + 2y = 0`

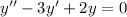
The characteristic equation

`r^2 - 3r + 2 = (r - 1) (r - 2) = 0`

has roots at
`r=1` and
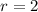`r=2`. Then the characteristic solution is

`y = C_1 e^x + C_2 e^(2x)`

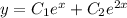
For nonhomogeneous ODE (1),

`y'' - 3y' + 2y = e^x`

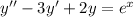
consider the ansatz particular solution

`y = axe^x \implies y' = a(x+1) e^x \implies y'' = a(x+2) e^x`

Substituting this into (1) gives

`a(x+2) e^x - 3 a (x+1) e^x + 2ax e^x = e^x \implies a = -1`

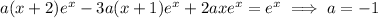
For the nonhomogeneous ODE (2),

`y'' - 3y' + 2y = e^(2x)`

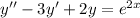
take the ansatz

`y = bxe^(2x) \implies y' = b(2x+1) e^(2x) \implies y'' = b(4x+4) e^(2x)`

Substitute (2) into the ODE to get

`b(4x+4) e^(2x) - 3b(2x+1)e^(2x) + 2bxe^(2x) = e^(2x) \implies b=1`

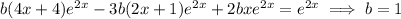
Lastly, for the nonhomogeneous ODE (3)

`y'' - 3y' + 2y = e^(-x)`

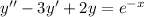
take the ansatz

`y = ce^(-x) \implies y' = -ce^(-x) \implies y'' = ce^(-x)`

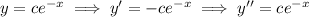
and solve for
`c`.

`ce^(-x) + 3ce^(-x) + 2ce^(-x) = e^(-x) \implies c = \frac16`

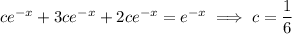
Then the general solution to the ODE is

`\boxed{y = C_1 e^x + C_2 e^(2x) - xe^x + xe^(2x) + \frac16 e^(-x)}`