Question

hi i was just wondering how to do this question (attached below) - ive been trying to figure it out for ages but have had no luck - could use some help! thanks

Answer 1

Answer: 88°

Explanation:

We know that the ratio of ∠DCB : ∠ACD is 3:1. In other words, ∠DCB is
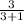`(3)/(3+1)`, or
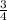`(3)/(4)` of the whole angle (i.e., ∠ACB), while ∠ACD is
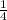`(1)/(4)` of the whole angle.

To easily find ∠ACB, which is the sum of both angles, we can add up all the angles of
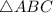`\triangle ABC` and set it equal to 180°.

`m\angle A + m\angle B + m\angle ACB = 180\\75+53+m\angle ACB=180\\128+m\angle ACB=180\\m\angle ACB=52`

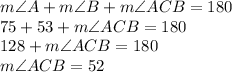
From here, we can calculate ∠BCD by multiplying the value of ∠ACB by three-fourths.

`m\angle BCD = (3)/(4)(m\angle ACB)\\m\angle BCD = (3)/(4)(52)\\m\angle BCD = 39`

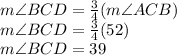
Similar to what we did to get the measure of ∠ACB, we can add up all the angles measures of
`\triangle DBC` to get the measure of ∠BDC.

`m\angle B + m\angle BDC + m\angle BCD = 180\\53+m\angle BDC + 39= 180\\92+ m\angle BDC=180\\m\angle BDC = 88`

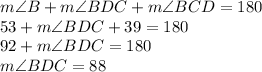
The measure of ∠BDC is 88°.