Let
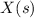 and
and
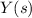 denote the Laplace transforms of
denote the Laplace transforms of
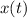 and
and
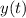 .
.
Taking the Laplace transform of both sides of both equations, we have
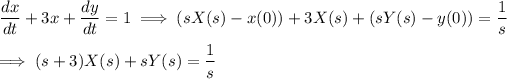
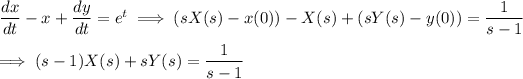
Eliminating
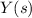 , we get
, we get
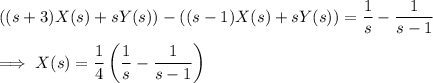
Take the inverse transform of both sides to solve for
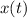 .
.
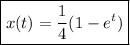
Solve for
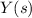 .
.
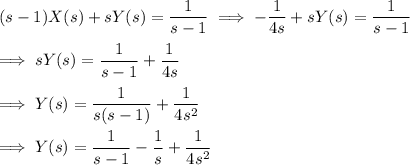
Taking the inverse transform of both sides, we get
