Best guess for the function is
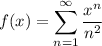
By the ratio test, the series converges for
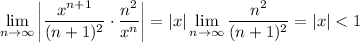
When
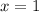 ,
,
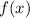 is a convergent
is a convergent
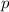 -series.
-series.
When
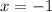 ,
,
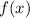 is a convergent alternating series.
is a convergent alternating series.
So, the interval of convergence for
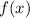 is the closed interval
is the closed interval
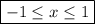 .
.
The derivative of
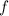 is the series
is the series
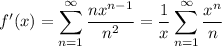
which also converges for
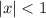 by the ratio test:
by the ratio test:
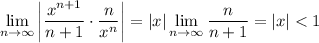
When
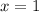 ,
,
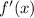 becomes the divergent harmonic series.
becomes the divergent harmonic series.
When
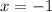 ,
,
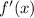 is a convergent alternating series.
is a convergent alternating series.
The interval of convergence for
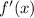 is then the closed-open interval
is then the closed-open interval
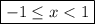 .
.
Differentiating
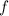 once more gives the series
once more gives the series
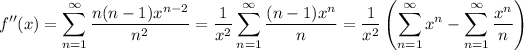
The first series is geometric and converges for
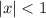 , endpoints not included.
, endpoints not included.
The second series is
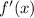 , which we know converges for
, which we know converges for
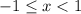 .
.
Putting these intervals together, we see that
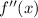 converges only on the open interval
converges only on the open interval
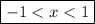 .
.