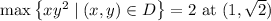Assuming you mean
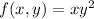 over the domain
over the domain
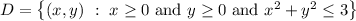
we first observe that
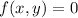 for all
for all
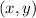 on the coordinate axes.
on the coordinate axes.
There are no critical points elsewhere in the interior of
 , since
, since
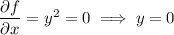
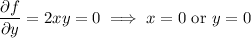
Parameterize the circular arc boundary by
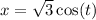 and
and
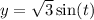 , where
, where
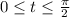 . Then
. Then
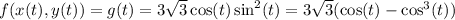
Find the critical points of
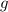 .
.
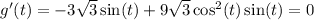
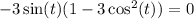
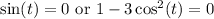
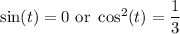
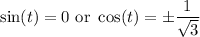
In the first case, we get
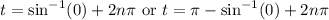
where
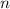 is an integer; the only solution on the boundary of
is an integer; the only solution on the boundary of
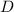 is
is
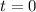 corresponding to the point
corresponding to the point
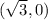 .
.
In the second case, we get
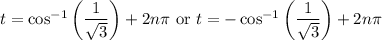
with only one relevant solution at
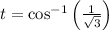 corresponding to
corresponding to
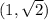 .
.
In the third case, we get
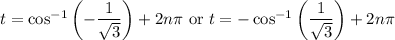
but there is no
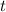 in this family of solutions such that
in this family of solutions such that
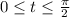 .
.
So, we find
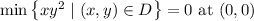
(but really any point on either axis works)