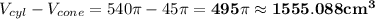Question

The figure shows a cylinder of diameter 12cm and height = 15cm. A hole in the shape of cone is bored into one of its end. If the cone has diameter equal to half of the diameter of the cylinder. find the volume of the remaining solid.​

Answer 1

`\bold{495\pi} \approx \bold{1555.088 cm^3}`

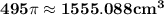
Explanation:

There was no figure but the question is clear

Volume of a cylinder is given by the formula
`\bold{\pi r^2h}\\`

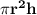
where r is radius of base of cylinder, h is the height

Volume of a cone is given by
`\bold{(1)/(3) \pi r^2 h}`

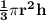
where r is the radius of base of cone, h is the height

The radius of the cylinder =
`(1)/(2)`(diameter) =
`(1)/(2)`(12) = 6cm

Height of cylinder = 15cm

Volume of cylinder
`V_(cyl) = \pi (6)^2 15 = \pi (36)15 = \bold{540\pi}`

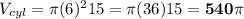
Radius of cone =
`(1)/(2)` (radius of cylinder) =
`(1)/(2)`(6) = 3 cm

Height of cone same as height of cylinder = 15cm

Volume of cone,
`V_(cone) = (1)/(3)\pi r^2 h = (1)/(3)\pi (3)^2 15 = (1)/(3)(9)15\pi = \bold{45\pi}\\`

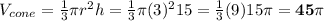
Difference is the volume of the remaining solid

`V_(cyl) - V_(cone) = 540\pi - 45\pi = \bold{495\pi} \approx \bold{1555.088 cm^3}`