Question

The data set below has 7 values. Find the mean absolute deviation for the data set. If necessary, round your answer to the nearest hundredth. 20, 16, 21, 16, 22, 16, 15

Answer 1

2.57

Explanation:

The mean absolute deviation(MAD) of a data set is given by the formula

`$ MAD =(1)/(n) \sum_(i=1)^n |x_i-\bar{x}|$`

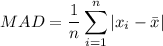
n = number of data set values. Here n=7

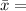`\bar{x}=`mean of the data set values =
`(20+16+21+16+22+16+ 15)/7 = 126/7 = 18`

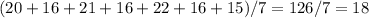
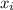`x_(i)` are the n individual values

Substituting in the summation we get

MAD =
`(1)/(7) |20-18| + |16-18| + |21-18| + |16-18| + |22-18| + |16-18| + |15-18|\\= (2 + 2 + 3 + 2 + 4+ 2 + 3)/7\\= 18/7 = 2.571428 \\`

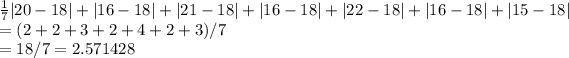
Rounded to the nearest hundredth, the answer is 2.57