Answer: 36.4 units (choice A)
===========================================================
Step-by-step explanation:
Let's use the distance formula to find the distance from D to E
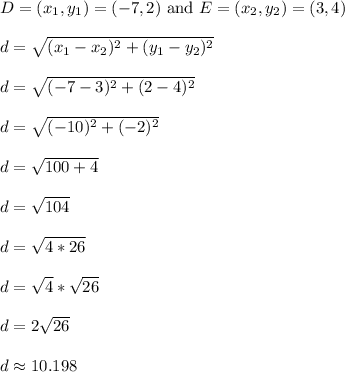
Note: uppercase D refers to the point, while lowercase d is the distance from D to E.
The length of segment DE is roughly 10.198 units long.
----------------
Repeat for the distance from E to F.
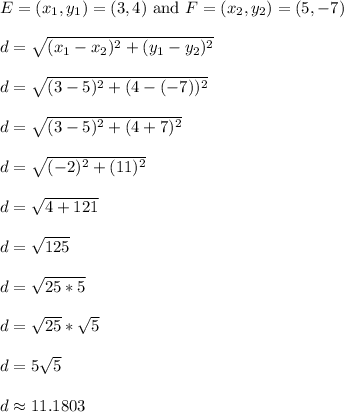
Segment EF is roughly 11.1803 units long.
----------------
Repeat for the distance from F to D.
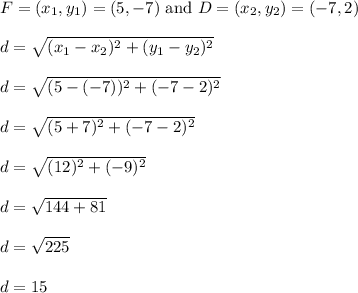
Unlike the others, this result is exact.
----------------
Add up the three segment lengths to get the perimeter
DE + EF + FD
10.198 + 11.1803 + 15
36.3783
The perimeter is approximately 36.3783 units which rounds to 36.4
The answer has been confirmed with GeoGebra.