Answer:
98 degrees
Explanation:
In a quadrilateral, we have 4 angles whose sum is 360 degrees which can be derived using the Exterior Angle Sum Theorem which essentially states that any convex polynomial will have a sum of 360 degrees for it's exterior angles.
Since we know that two of the angles are equal, we can just represent angle A and D as "x", and since they're congruent, and there is two of them, the sum can be represented as "2x"
So using all the known values we can set up the following equation:
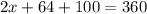
Simplify on the left side
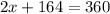
Subtract 164 from both sides
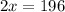
Divide both sides by 2
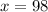
Since we know that "x" represents both angle A and B, then the angle A is 98 degrees.