Question

Please help!!!
maths functions

Answer 1

a) A = (2, 10) and B = (-3, 0)

b) C = (-5, -4) and D = (-5, -32)

Step-by-step explanation:

a) To determine the coordinates of A and B, find the intersection points of the line "y = 2x + 6" and curve "y = -2x² + 18".

Solve the equation's simultaneously:

y = y

⇒ 2x + 6 = -2x² + 18

⇒ 2x² + 2x + 6 - 18 = 0

⇒ 2x² + 2x - 12= 0

⇒ 2x² + 6x - 4x - 12 = 0

⇒ 2x(x + 3) - 4(x + 3) = 0

⇒ (2x - 4)(x + 3) = 0

⇒ 2x - 4 = 0, x + 3 = 0

⇒ x = 2, x = -3

Then find value of y at this x points,

at x = 2, y = 2(2) + 6 = 10

at x = -3, y = 2(-3) + 6 = 0

Intersection points: A(2, 10) and B(-3, 0)

b) Given that CD = 28 units. Also stated parallel to y axis so x coordinates for both will be same but differ in y coordinate.

`2x + 6 = -2x^2 + 18 + 28`

`-2x^2 + 18 + 28-2x - 6 = 0`

`-2x^2-2x+40=0`

`-2x^2-10x+8x+40=0`

`-2(x+5)+8(x+5)=0`

`(-2x+8)(x+5)=0`

`x = -5, 4`

`\leftrightarrow \sf C(-5, y_2), \ D(-5, y_2)`

Find y value for Point C : 2x + 6 = 2(-5) + 6 = -4

Find y value for Point D : -2x² + 18 = -2(-5)² + 18 = -32

`\sf \rightarrow Point \ C = (-5, -4)\\ \\\rightarrow Point \ D = (-5, -32)`

Answer 2

Point A: (2, 10)

Point B: (-3, 0)

Point C: (-5, -4)

Point D: (-5, -32)

Step-by-step explanation:

Part (a)

Points A and B are the points of intersection between the two graphs.

Therefore, to find the x-values of the points of intersection, substitute one equation into the other and solve for x:

`\implies 2x+6=-2x^2+18`

`\implies 2x^2+2x-12=0`

`\implies 2(x^2+x-6)=0`

`\implies x^2+x-6=0`

`\implies x^2+3x-2x-6=0`

`\implies x(x+3)-2(x+3)=0`

`\implies (x-2)(x+3)=0`

`\implies x=2, -3`

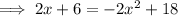
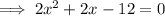
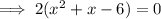
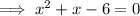
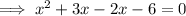
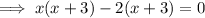
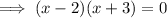
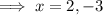
From inspection of the graph:

• The x-value of point A is positive ⇒ x = 2
• The x-value of point B is negative ⇒ x = -3

To find the y-values, substitute the found x-values into either of the equations:

`\begin{aligned} \textsf{Point A}: \quad 2x+6 & =y\\2(2)+6 & =10\\ \implies & (2, 10)\end{aligned}`

`\begin{aligned} \textsf{Point B}: \quad -2x^2+18 & =y\\-2(-3)^2+18 & =0\\ \implies & (-3,0)\end{aligned}`

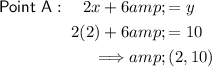
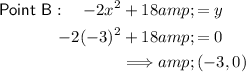
Therefore, point A is (2, 10) and point B is (-3, 0).

Part (b)

If the distance between points C and D is 28 units, the y-value of point D will be 28 less than the y-value of point C. The x-values of the two points are the same.

Therefore:

`\textsf{Equation 1}: \quad y=2x+6`

`\textsf{Equation 2}: \quad y-28=-2x^2+18`

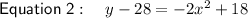
As the x-values are the same, substitute the first equation into the second equation and solve for x to find the x-value of points C and D:

`\implies 2x+6-28=-2x^2+18`

`\implies 2x^2+2x-40=0`

`\implies 2(x^2+x-20)=0`

`\implies x^2+x-20=0`

`\implies x^2+5x-4x-20=0`

`\implies x(x+5)-4(x+5)=0`

`\implies (x-4)(x+5)=0`

`\implies x=4,-5`

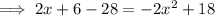
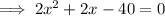
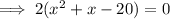
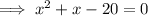
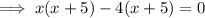
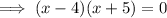
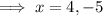
From inspection of the given graph, the x-value of points C and D is negative, therefore x = -5.

To find the y-value of points C and D, substitute the found value of x into the two original equations of the lines:

`\begin{aligned} \textsf{Point C}: \quad 2x+6 & =y\\2(-5)+6 & =-4\\ \implies & (-5,-4)\end{aligned}`

`\begin{aligned} \textsf{Point D}: \quad -2x^2+18 & = y \\ -2(-5)^2+18 & =-32\\ \implies & (-5, -32)\end{aligned}`

Therefore, point C is (-5, -4) and point D is (-5, -32).