Explanation:
First thing first, let find the x value of where P and Q both meet y=5, we know that y=5, and y=2x^2+7x-4, so using transitive law,
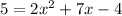
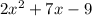
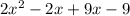
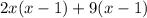
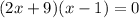
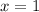
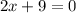
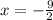
Now, to find the gradient of the curve let take the derivative of both sides
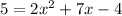
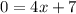
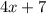
Plug in -9/2, let call that point P
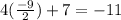
Plug in 1, let call that point Q
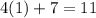
So the gradient of the curve at point P (-9/2,5) is -11
The gradient of the curve at point Q (1,5) is 11.