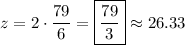Let
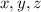 denote the amounts (in liters) of the 20%, 30%, and 60% solutions used in the mixture, respectively.
denote the amounts (in liters) of the 20%, 30%, and 60% solutions used in the mixture, respectively.
The chemist wants to end up with 72 L of solution, so
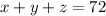
while using twice as much of the 60% solution as the 30% solution, so
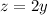
The mixture needs to have a concentration of 35%, so that it contains 0.35•75 = 26.25 L of pure acid. For each liter of acid solution with concentration
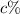 , there is a contribution of
, there is a contribution of
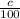 liters of pure acid. This means
liters of pure acid. This means

Substitute
 into the total volume and acid volume equations.
into the total volume and acid volume equations.
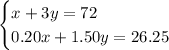
Solve for
 and
and
 . Multiply both sides of the second equation by 5 to get
. Multiply both sides of the second equation by 5 to get
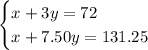
By elimination,
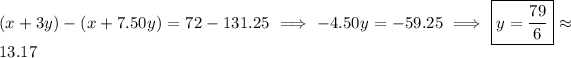
so that
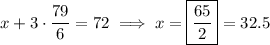
and