Answer:
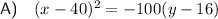
B) Focus = (40, -9)
Directrix: y = 41
Axis of symmetry: x = 40
Explanation:
The x-intercepts of a parabola are the points at which the curve intercepts the x-axis (when y = 0).
The x-coordinate of the vertex of a parabola is halfway between the x-intercepts.
The y-coordinate of the vertex if the minimum or maximum height of the parabola.
Part A
A jumping spider's movement is modeled by a parabola.
Define the variables:
- x = horizontal distance of the spider
- y = height of the spider
From the information given:
- x-intercepts = (0, 0) and (80, 0)
- vertex = (40, 16)
Standard form of a parabola with a vertical axis of symmetry:

- Vertex: (h, k)
- Focus: (h, k+p)
- Directrix: y = (k-p)
- Axis of symmetry: x = h
If p > 0, the parabola opens upwards, and if p < 0, the parabola opens downwards.
Substitute the vertex (40, 16) and one of the x-intercept points (0, 0) into the formula and solve for p:
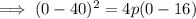
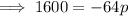
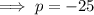
Substitute the vertex and the found value of p into the formula:
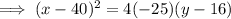
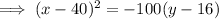
Part B
Given:
- Vertex = (40, 16) ⇒ h = 40 and k = 16
- p = -25
Substitute the given values into the formulas for focus, directrix and axis of symmetry:
Focus
⇒ (h, k+p)
⇒ (40, 16 + (-25)))
⇒ (40, -9)
Directrix
⇒ y = (k-p)
⇒ y = (16 - (-25))
⇒ y = 41
Axis of symmetry
⇒ x = h
⇒ x = 40