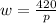Answer:
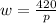
Explanation:
So generally a direct proportion can be expressed as:
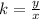
essentially where the y/x is equal to some constant value.
Whenever you have an inverse proportion, you can generally express it as:
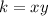
where the product of x and y is equal to some constant value.
So we can check for inverse proportion, by seeing if the xy product is constant
1 * 420 = 420
2 * 210 = 420
3 * 140 = 420
Since the xy (or technically wp, or in general the product of the independent variable and dependent variable) product is constant, this relationship can generally be expressed as:
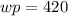
We can divide both sides by p, so we can isolate the dependent variable (p)