Answer:
Approximately
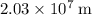 .
.
Step-by-step explanation:
Assume that the radius of this orbit is
 .
.
Let
 denote the mass of this satellite and let
denote the mass of this satellite and let
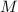 denote the mass of the Earth. At a distance of
denote the mass of the Earth. At a distance of
 from the center of the earth, the magnitude of the gravitational attraction on this satellite would be
from the center of the earth, the magnitude of the gravitational attraction on this satellite would be
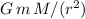 .
.
The question implies that the gravitational pull from the earth is the only significant force on this satellite. Hence, the net force on this satellite would be also
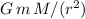 .
.
The acceleration of this satellite would thus be
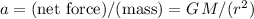 .
.
Let
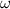 denote the angular velocity of this satellite. Since this satellite in in a circular motion, the acceleration on this satellite would need to satisfy
denote the angular velocity of this satellite. Since this satellite in in a circular motion, the acceleration on this satellite would need to satisfy
 .
.
In other words:
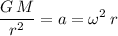 .
.
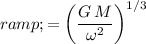 .
.
The question asks for a rotation of
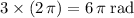 within a day, which is
within a day, which is
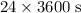 . The angular velocity of this satellite should be:
. The angular velocity of this satellite should be:
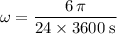 .
.
Substitute this value into the expression for
 and evaluate:
and evaluate:
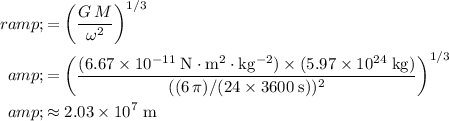 .
.
(Note that
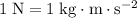 .)
.)