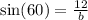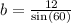Question

asked May 4, 2023 135k views

2 Answers

Sumesh TG · Answer 1 · 2023-05-05T13:43:02+0000

Answer:

Below in bold.

Explanation:

The first triangle is a 30-60-90 triangle,

so the sides are in the ratio 2 : 1 : √3, where 2 is the hypotenuse, the 1 is adjacent to 60 degree angle and the √3 is opposite the 60 degree angle.

So x = 1/2 * 32 = 16

and y = 16√3 or 27.71 to nearest hundredth.

The second one is the same special triangle, so

√3/2 = 12/b

b = 24/√3

= 8√3 or 13.86 to nearest hundredth.

a = 1/2 b = 4√3 or 6.93 to nearest hundredth.

Mathias Verhoeven · Answer 2 · 2023-05-09T02:12:26+0000

Explanation:

This is trigonometry. Focusing on Y initially, we can see that Y is the opposite, and 32 is the hypotenuse. Therefore, we must use sin:

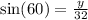
$\sin(60) = (y)/(32)$

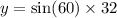
$y = \sin(60) * 32$

$y \approx28$

Next X. We can see that X is the adjacent, and 32 is the hypotenuse, so we must use cos:

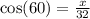
$\cos(60) = (x)/(32)$

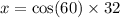
$x = \cos(60) * 32$

x = 16

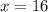
Now let's look at A. We can see that a is the adjacent, and 12 is the opposite, so we must use tan:

$\tan(60) = (12)/(a)$

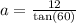
$a = (12)/( \tan(60) )$

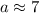
$a \approx7$

Now, B. We can see that B is the hypotenuse, and 12 is the opposite, so we must use sin:

$\sin(60) = (12)/(b)$

$b = (12)/( \sin(60) )$

$b \approx14$

Please log in or register to add a comment.