Question

1+r+r²+...........+r^n+1=1-r^n/1-r​

mathematical induction mesthod

Answer 1

Answer + Step-by-step explanation:

the correct question:

For r ≠ 1 ,Prove using the mathematical induction method that :

`1+\cdots+r^n =(1-r^(n+1))/(1-r)`

………………………………………………………………………………………………………………

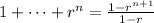
for n = 0 :

1⁰ = 1 and (1 - r⁰⁺¹)/(1 - r) = (1 - r)/(1 - r) = 1

Then the property is true for n = 0.

For n ≥ 0 :

Suppose

`1+\cdots+r^n =(1-r^(n+1))/(1-r)`

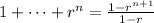
And prove that

`1+\cdots+r^(n+1) =(1-r^(n+2))/(1-r)`

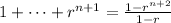
Since :

`1+\cdots+r^(n+1) =(1+\cdots+r^n)+r^(n+1)`

Then

`1+\cdots+r^n+r^(n+1) =(1-r^(n+1))/(1-r)+r^(n+1)`

`= (1-r^(n+1)+r^(n+1)(1-r))/(1-r)`

`= (1-r^(n+2))/(1-r)`

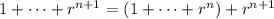
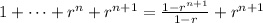
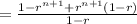
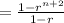
Then according to the mathematical induction method

`1+\cdots+r^n =(1-r^(n+1))/(1-r)`

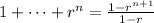
Where n is a natural number and r ≠ 1.