Answer:
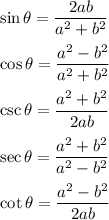
Explanation:
We are given that:
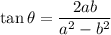
To find other trigonometric ratios, first, we have to know that there are total 6 trigonometric ratios:

Since we are given tangent relation, we know that
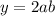 and
and
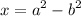 , all we have to do is to find hypotenuse or radius (r) which you can find by applying Pythagoras Theorem.
, all we have to do is to find hypotenuse or radius (r) which you can find by applying Pythagoras Theorem.
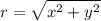
Therefore:
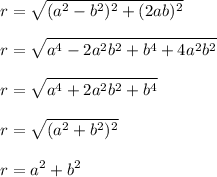
Now we can find other trigonometric ratios by simply substituting the given information below:
Hence:
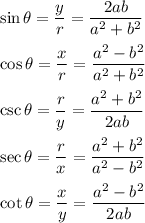
will be other trigonometric ratios.