Question

In AABC, m/A = 15°, a = 9, and b = 12. Find c to the nearest tenth.

A. 20.0 B. 17.4 C. 8.4 D. 11.5​

Answer 1

Explanation:

This is a Law of Sines problem. The expanded formula is

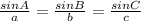`(sinA)/(a) =(sinB)/(b) =(sinC)/(c)` where the capital letters are the angles and the lowercase letters are the side lengths. We only use 2 of these ratios at a time. And in order to do that, we can only have one unknown per set of ratios. I have angle A and side a, so I'll use that ratio, but I don't have angle C to help me find side c. I also don't have angle B. But I do have side b, so I'll use the A and B sin stuff and then solve for C indirectly.

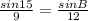`(sin15)/(9) =(sinB)/(12)` to solve for angle B. Cross multiply:

`sinB=(12sin15)/(9)`

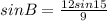
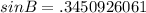`sinB=.3450926061` Use the inverse and sin keys on your calculator (in degree mode) to get that

B = 20.2°. Now that we have that, we can find the measure of angle C:

180 - 15 - 20.2 = 144.8°

Now we can use the sin ratio involving the angle C, side c (our unknown), and angle A and side a:

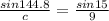`(sin144.8)/(c)=(sin15)/(9)` and cross multiply to solve for c:

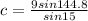`c=(9sin144.8)/(sin15)` gives us that

c = 20.0