Question

The elimination method is ideal for solving this system of equations. By which number must you multiply the second equation to eliminate the

y-varlable, and what is the solution for this system?
x+3y=42
2x-y=1

Answer 1

Answers:

• Triple each side of the 2nd equation
• The solution is (x,y) = (45/7, 83/7) meaning that x = 45/7 and y = 83/7 pair up together. The fractions are reduced as much as possible.

=======================================================

Step-by-step explanation:

The 3y in the first equation must add to -3y so the y terms go away. We have -y in the second equation, which is why we triple everything in that equation

2x-y = 1 becomes 6x - 3y = 3 after tripling everything. This is the same as multiplying both sides by 3.

This is the updated equivalent system

`\begin{cases}x+3y = 42\\6x-3y = 3\end{cases}`

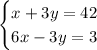
Add the terms straight down

• x+6x becomes 7x
• 3y+(-3y) becomes 0y or 0. The y variables are eliminated.
• The right hand sides 42 and 3 add to 45

We have the equation 7x = 45 which solves to x = 45/7.

Unfortunately it doesn't turn into a nice single whole number because 45 isn't a multiple of 7. So I would leave it as a fraction.

Optionally you could note that 45/7 = 6.42857 approximately. But I prefer the fraction form since it's most exact.

--------------

Use this x value to find y. Pick any equation involving x and y. Plug in that x value and solve for y.

x + 3y = 42

45/7 + 3y = 42

3y = 42 - 45/7

3y = 42*(7/7) - 45/7

3y = 294/7 - 45/7

3y = (294 - 45)/7

3y = 249/7

y = (249/7)*(1/3)

y = 83/7

Like with x, we also don't get a nice whole number.

I used WolframAlpha to confirm the solutions. GeoGebra is another tool you could use.