Answer:
a
Explanation:
the equation of a line in slope- intercept form is
y = mx + c ( m is the slope and c the y- intercept )
calculate m using the slope formula
m =
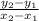
with (x₁, y₁ ) = (4, - 1 ) and (x₂, y₂ ) = (- 2, 3 )
m =
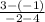 =
=
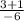 =
=
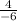 = -
= -
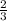 , then
, then
y = -
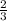 x + c ← is the partial equation
x + c ← is the partial equation
to find c substitute either of the 2 points into the partial equation
using (- 2, 3 ) , then
3 =
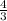 + c ⇒ c = 3 -
+ c ⇒ c = 3 -
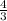 =
=
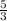
y = -
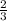 x +
x +
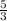 ← in slope- intercept form
← in slope- intercept form
multiply through by 3 to clear the fractions
3y = - 2x + 5 ( subtract - 2x + 5 from both sides )
2x + 3y - 5 = 0 ← in general form