Question

Example 2.11: Solve the following
a) 4x² +10x = 6

Answer 1

Answer: x = 3 or (-1/2)

Explanation:

Given equation

4x² + 10x = 6

Subtract 6 on both sides

4x² + 10x - 6 = 6 - 6

4x² + 10x - 6 = 0

Use cross-multiplication to factorize the quadratic

Starting with:

2x -6

2x 1

This gives us:

(2x - 6) (2x + 1) = 0

Assume each value in the parenthesis to be 0

PART I:

2x - 6 = 0 ⇒ Given equation

2x - 6 + 6 = 0 + 6 ⇒ Add 6 on both sides

2x / 2 = 6 / 2 ⇒ Divide 2 on both sides

`\boxed{x=3}`

PART II:

2x + 1 = 0 ⇒ Given equation

2x + 1 - 1 = 0 - 1 ⇒ Subtract 1 on both sides

2x / 2 = -1 / 2 ⇒ Divide 2 on both sides

`\boxed{x=-(1)/(2) }`

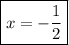
Hope this helps!! :)

Please let me know if you have any questions

Answer 2

`\huge\boxed{\sf \{-3, 1/2\}}`

Explanation:

Given equation:

4x² + 10x = 6

Take 2 common

2(2x² + 5x) = 6

Divide 2 to both sides

2x² + 5x = 3

Subtract 3 to both sides

2x² + 5x - 3 = 0

Using mid-term break

2x² + 6x - x - 3 = 0

Take common

2x(x + 3) - 1(x + 3) = 0

Take (x + 3) common

(x + 3)(2x - 1) = 0

Either,

x + 3 = 0 OR 2x - 1 = 0

x = -3 OR 2x = 1

x = -3 OR x = 1/2

Solution Set = {-3, 1/2}

`\rule[225]{225}{2}`