Question

Please help im stuck its math

Answer 1

y = 5x - 6

Explanation:

We are given a line, which is parallel to the line y=5x+3.

We also know that this line passes through the point (3,9).

We want to find the equation of this line.
Parallel lines have the same slopes, yet different y intercepts.
So, let's find the slope of the line y=5x+3.

The line is written in slope-intercept form, which is y=mx+b, where m is the slope and b is the value of y at the y intercept.

As 5 is in the place of where the slope (m) is, 5 is the slope of the line.

It is also the slope of the line parallel to it (which is the line we are trying to find).

We can write the equation of this new line in slope-intercept form as well, which is also the format your system wants.

Before we write the equation of the line in slope-intercept form, we can write it in point-slope form, then convert it into slope-intercept form.

Point-slope form is
`y-y_1=m(x-x_1)`, where m is the slope and
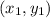`(x_1, y_1)` is a point.

As we have already found the slope (5), we can immediately plug it into the formula.

`y-y_1=5(x-x_1)`

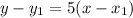
Now, remember that we were also given a point, that passes through the line. This point is (3,9).

We can use its values in the formula.

Substitute 3 as
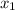`x_1` and 9 as
`y_1`.

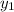y - 9 = 5(x-3)

Now, we have written the line in point-slope form.

However, we're not done yet; remember that we want it in slope-intercept form.

We can solve the equation for y to get slope-intercept form.

So, on the right, open up the parentheses and distribute 5 to both x and -3.

y - 9 = 5x - 15

Now add 9 to both sides.

y = 5x - 6