Question

PLEASE HELP its math

Answer 1

y = 3x + 6

Explanation:

We are given a line.

We know this line is parallel to the line y=3x+2, and passes through (1, 9).
We want find the equation of this line.

Parallel lines have the same slopes.

So, let's find the slope of y=3x+2.

The line is written the format y=mx+b, where m is the slope and b is the value of y at the y intercept.

As 3 is in the place of where m (the slope) is, the slope of the line is 3.

It is also the slope of the line parallel to it.

We should write the equation of the line parallel y=3x+2 in slope-intercept form as well, however, before we do that, we can write the line in point-slope form, and then convert it to slope-intercept form.

Point-slope form is given as
`y-y_1=m(x-x_1)`, where m is the slope and
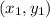`(x_1,y_1)` is a point.

We can substitute 3 as m in the formula, as we know that is the slope of the line

`y-y_1=3(x-x_1)`

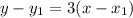
Recall that we were given the point (1, 9), which also belongs to (it passes through) the line.

Therefore, we can use its values in the formula.

Substitute 1 as
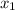`x_1` and 9 as
`y_1`.

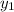y - 9 = 3(x-1)

We can now convert the equation into slope intercept form.

Notice how y is by itself in slope-intercept form; this means we'll need to solve the equation for y.

Start by distributing 3 to both x and -1.

y - 9 = 3x - 3

Now add 9 to both sides.

y = 3x + 6