Question

If f(x) = 5x, what is f¹(x)?

Answer 1

C

Explanation:

For any function x, inverse will = 1/x. so the answer is C

Answer 2

C.
`f^(-1)(x) = (1)/(5) x`

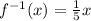
Explanation:

The question is asking to find
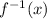`f^(-1)(x)` of f(x)=5x, which is the same as finding the inverse of the function.

To find the inverse of a function, we first need to replace f(x) with y.

The function will therefore be:

y = 5x

Now, we solve the equation for x.

So divide both sides by 5.

y = 5x

÷5 ÷5

_________

`(y)/(5) = x`

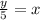
Now, we replace x with y and y with x.

`(x)/(5) = y`

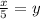
Finally, we replace y with
`f^(-1)(x)`.

`(x)/(5) = f^(-1)(x)`

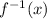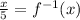
We can re-write this though, to make it easier to read.

We can write
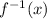`f^(-1)(x)` first, and rewrite
`(x)/(5)` as
`(1)/(5)x`.

`f^(-1)(x) = (1)/(5) x`

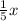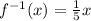
Therefore, the answer is C.