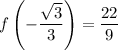Your answers seem to be on the right track. These online homework apps can be picky about the answer they accept, though.
Given
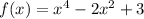 , we have derivative
, we have derivative

with critical points when
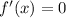 ; this happens when
; this happens when
 or
or
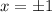 .
.
We also have second derivative
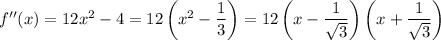
with (possible) inflection points when
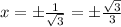 .
.
Intercept
If "intercept" specifically means
 -intercept, what you have is correct. Setting
-intercept, what you have is correct. Setting
 gives
gives
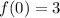 , so the intercept is the point (0, 3).
, so the intercept is the point (0, 3).
They could also be expecting the
 -intercepts, in which case we set
-intercepts, in which case we set
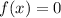 and solve for
and solve for
 . However, we have
. However, we have
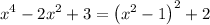
and
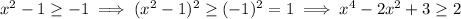
so there are no
 -intercepts to worry about.
-intercepts to worry about.
Relative minima/maxima
Check the sign of the second derivative at each critical point.
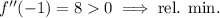
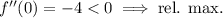
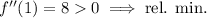
So we have two relative minima at the points (-1, 2) and (1, 2), and a relative maximum at (0, 3).
Inflection points
Simply evaluate
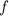 at each of the candidate inflection points found earlier.
at each of the candidate inflection points found earlier.