Compute the first two derivative.
Take note of the domain of
 . We must have
. We must have
 for the square root to be defined, so
for the square root to be defined, so
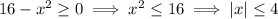
and
 exists only for
exists only for
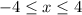 .
.
Intercepts
Set
 to find the
to find the
 -intercepts. The only one is (0, 0), since
-intercepts. The only one is (0, 0), since
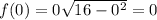
The first intercept you listed is not a valid intercept. One or both coordinates must be 0.
Set
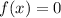 and solve for
and solve for
 to find
to find
 -intercepts. We already found (0, 0); there are two others at (-4, 0) and (4, 0).
-intercepts. We already found (0, 0); there are two others at (-4, 0) and (4, 0).
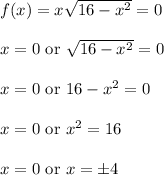
The instructions say to list these in order from smallest to largest by
 -coordinate first, then by
-coordinate first, then by
 -coordinate. So the proper order of the intercepts would be (-4, 0), (0, 0), and (4, 0).
-coordinate. So the proper order of the intercepts would be (-4, 0), (0, 0), and (4, 0).
Relative minima/maxima
Find the critical points. We have
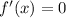 when
when
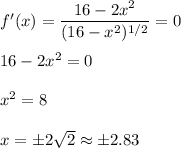
and
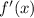 is undefined when
is undefined when
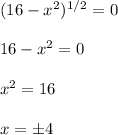
Check the sign of the second derivative at the first two critical points.

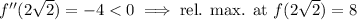
For posterity, we should also check the value of
 at the endpoints of the domain.
at the endpoints of the domain.

So
 has a relative minimum at (-2.83, -8) and a relative maximum at (2.83, 8).
has a relative minimum at (-2.83, -8) and a relative maximum at (2.83, 8).
Inflection points
We have
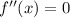 for
for
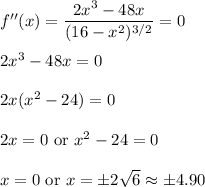
The two non-zero solutions fall outside the domain, so the only inflection point is (0, 0).