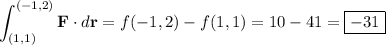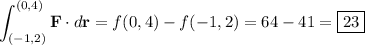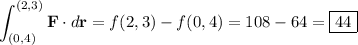(a) We want to find a scalar function
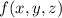 such that
such that
 . This means
. This means
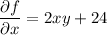

Looking at the first equation, integrating both sides with respect to
 gives
gives
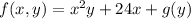
Differentiating both sides of this with respect to
 gives
gives
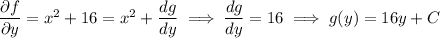
Then the potential function is
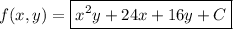
(b) By the FTCoLI, we have