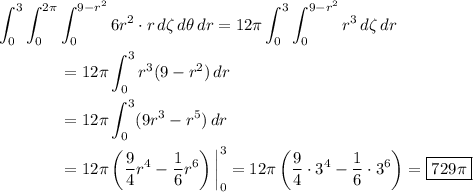Compute the divergence of
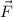 .
.
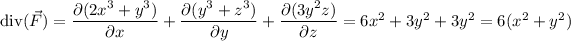
By the divergence theorem, the integral of
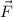 across
across
 is equivalent to the integral of
is equivalent to the integral of
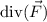 over the interior of
over the interior of
 , so that
, so that
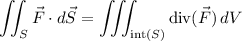
The paraboloid meets the
 -plane in a circle with radius 3, so we have
-plane in a circle with radius 3, so we have

and
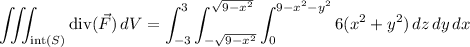
Convert to cylindrical coordinates, with
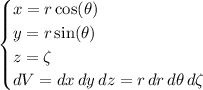
so that
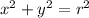 , and the domain of integration is the set
, and the domain of integration is the set

Now compute the integral.