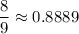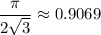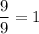a. By replacing
 with
with
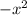 in the power series, we get
in the power series, we get
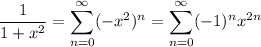
Integrate both sides to recover
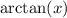 on the left.
on the left.
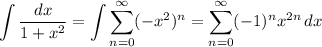
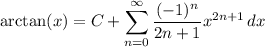
By letting
 on both sides, we find
on both sides, we find
 , so that
, so that

Then dividing both sides by
 gives
gives

b. Let
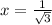 . Then
. Then
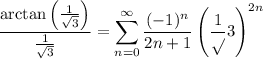

Taking the first few terms from the infinite series, we can approximate
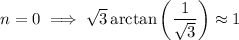
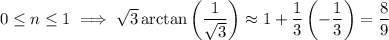
which together suggest the value we want is bounded between 8/9 and 9/9 = 1, hence
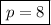 .
.
Since the series is alternating and converges on
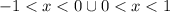 ,
,
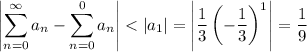
and
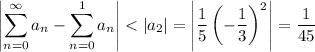
which tells us the first approximation is off by at most 1/9 from the actual value of
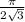 , whereas the second approximation is off by at most 1/45 from the actual value. In other words, the second approximation is closer, so
, whereas the second approximation is off by at most 1/45 from the actual value. In other words, the second approximation is closer, so
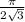 is closer to
is closer to
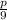 :
: