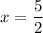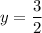System of Equations
There are two methods of solving systems of equations:
Substitution is where we substitute one equation into the other by isolating a certain variable, or a group of terms.
Elimination is where we subtract the two equations. Before doing this, we may have to multiply one equation by a certain number to make sure one variable cancels out.
Solving the Question
We're given the following equations:
Because they are organized in the same manner (i.e. x [operation] y [equals] number), it is easier for us to use elimination.
First, multiply the first equation by 2:
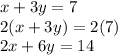
Now, subtract the second equation from the one we just created:
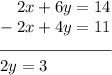
Solve for y:
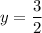
To solve for x, we can use substitution in the first equation:
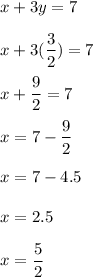
Answer