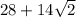Question

The hypotenuse of an isosceles right triangle is 14 centimeters longer than either of its legs. Find the exact length of each side.​ (Hint: An isosceles right triangle is a right triangle whose legs are the same​ length.)

Answer 1

The Pythagorean Theorem

The Pythagorean theorem states that:

`a^2+b^2=c^2`

• a and b are two legs of a right triangle
• c is the hypotenuse

The Quadratic Formula

`x=(-b\pm √(b^2-4ac))/(2a)`

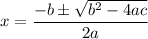
Solving the Question

Let a represent the length of one leg.

Because the hypotenuse is 14 cm longer than a leg, we can say that the hypotenuse's length is 14 + a.

Plug these into the Pythagorean theorem:

`a^2+b^2=c^2\\a^2+a^2=(14+a)^2\\2a^2=14^2+2(14)a+a^2\\2a^2=196+28a+a^2\\a^2=196+28a\\a^2-196-28a=0\\a^2-28a-196=0`

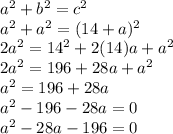
Factor using the quadratic formula:

`a=(-b\pm √(b^2-4ac))/(2a)`

`a=(-(-28)\pm √((-28)^2-4(1)(-196)))/(2(1))\\\\a=14\pm14√(2)\\\\a=14+14√(2)`

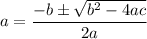
We know that it's plus because subtracting results in a negative value, and length cannot be negative.

This is the length of each side.

Because the hypotenuse is 14 cm longer, we can say that the hypotenuse is
`28+14√(2)`.

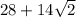Answer

Leg length =
`14+14√(2)`

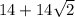
Hypotenuse length =
`28+14√(2)`