Let
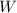 be the random variable for the winnings from playing the game once.
be the random variable for the winnings from playing the game once.
• There are 4 jacks in the deck, so you draw a jack with probability 4/52 = 1/13. In this case you "win" $1.25 - $1.75 = -$0.50.
• There are 4 queens, with draw probability 4/52 = 1/13 and winnings $3.25 - $1.75 = $1.50.
• There are 4 kings, with draw probability 4/52 = 1/13 and winnings $4.50 - $1.75 = $2.75.
• There are 4 aces, and 3 of these are not of the spade suit, so the probability of drawing any of these is 3/52 and you win $6.50 - $1.75 = $4.75.
• There is only 1 ace of spaces, with draw probability 1/52 and winnings $7.75 - $1.75 = $6.00.
• Adding these up, it follows that the probability of drawing any other card is 1 - (1/13 + 1/13 + 3/52 + 1/52) = 10/13, in which you have the privilege of "winning" -$1.75.
So, the probability mass function for
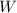 is
is

The expected winnings from playing one round of this game are
![\Bbb E[W] = \displaystyle \sum_w w\,\mathrm{Pr}(W=w)](https://img.qammunity.org/2023/formulas/mathematics/high-school/oqrlrrtq0fl392os4u5jfmvm3b5toeo8oc.png)
![\Bbb E[W] = (-\$0.50 + \$1.50 + \$2.75)/(13) + (3\cdot\$4.75)/(52) + (\$6.00)/(52) + (10\cdot(-\$1.75))/(13)](https://img.qammunity.org/2023/formulas/mathematics/high-school/pdmcbrmoiniaadsl5wkq6asmj53c6950fd.png)
![\Bbb E[W] \approx \boxed{-\$0.67}](https://img.qammunity.org/2023/formulas/mathematics/high-school/7bx9wlxi4hfk2g32qgp87odg06vi1zstwn.png)