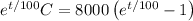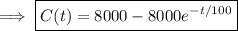Question

A 400 L tank is filled with pure water. A copper sulfate solution with a concentration of 20 g/L flows into the tank at a rate of 4 L/min. The thoroughly mixed solution is drained from the tank at a rate of 4 L/min. a. Write a differential equation (initial value problem) for the mass of the copper sulfate. b. Solve the differential equation

Answer 1

(a) Let
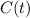`C(t)` denote the amount (in grams) of copper (II) sulfate (CuSO₄) in the tank at time
`t` minutes. The tank contains only pure water at the start, so we have initial value
`\boxed{C(0)=0}`.

CuSO₄ flows into the tank at a rate

`\left(20(\rm g)/(\rm L)\right) \left(4(\rm L)/(\rm min)\right) = 80 (\rm g)/(\rm min)`

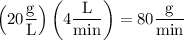
and flows out at a rate

`\left((C(t)\,\rm g)/(400\,\mathrm L + \left(4(\rm L)/(\rm min) - 4(\rm L)/(\rm min)\right) t)\right) \left(4(\rm L)/(\rm min)\right) = (C(t))/(100) (\rm g)/(\rm min)`

and hence the net rate of change in the amount of CuSO₄ in the tank is governed by the differential equation

`\boxed{(dC)/(dt) = 80 - \frac C{100}}`

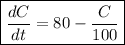
(b) This ODE is linear with constant coefficients and separable, so we have a few choices in how we can solve it. I'll use the typical integrating factor method for solving linear ODEs.

`(dC)/(dt) + \frac C{100} = 80`

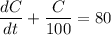
The integrating factor is

`\mu = \exp\left(\displaystyle \int (dt)/(100)\right) = e^(t/100)`

Distributing
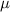`\mu` on both sides gives

`e^(t/100) (dC)/(dt) + \frac1{100} e^(t/100) C = 80 e^(t/100)`

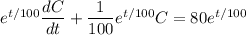
and the left side is now the derivative of a product,

`\frac d{dt} \left[e^(t/100) C\right] = 80 e^(t/100)`

Integrate both sides. By the fundamental theorem of calculus,

`e^(t/100) C = e^(t/100)C\bigg|_(t=0) + \displaystyle \int_0^t 80 e^(u/100)\, du`

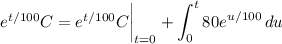
The first term on the right vanishes since
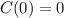`C(0)=0`. Then

`e^(t/100) C = 8000 \left(e^(t/100) - 1\right)`

`\implies \boxed{C(t) = 8000 - 8000 e^(-t/100)}`