Question

Consider the graph of the function f(x)=2^x which statements describe key features of function g if g(x)=3f(x)?

it's multiple choice, select all the correct answers:

y-intercept at (0,1)
y-intercept at (0,3)
horizontal asymptote of y=3
x-intercept at (3,0)
horizontal asymptote of y=0
no x-intercept

Answer 1

• y-intercept at (0,3)
• horizontal asymptote of y=0
• no x-intercept

Explanation:

The y-intercept of f(x) is (0,1), so the y-intercept of g(x) is (0,3).

f(x) has a horizontal asymptote at y=0. and so does g(x).

f(x) does not have an x-intercept, and neither does g(x).

Answer 2

y-intercept at (0, 3)

horizontal asymptote of y = 0

no x-intercept

Explanation:

Definitions

y-intercept: the point(s) at which the curve crosses the y-axis (when x=0).

x-intercept: the point(s) at which the curve crosses the x-axis (when y=0).

Asymptote: a line that the curve gets infinitely close to, but never touches.

Given function:

`f(x)=2^x`

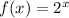
Properties of function f(x):

• y-intercept at (0, 1)
• As x → -∞, y → 0 therefore there is a horizontal asymptote at y=0 and no x-intercept (since the curve never crosses the x-axis).
• As x → ∞, y → ∞

`\textsf{If }g(x)=3f(x):`

`\implies g(x)=3(2)^x`

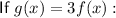
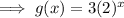
Properties of function g(x):

• y-intercept at (0, 3)
• As x → -∞, y → 0 therefore there is a horizontal asymptote at y=0 and no x-intercept (since the curve never crosses the x-axis).
• As x → ∞, y → ∞

Therefore the true statements are:

• y-intercept at (0, 3)
• horizontal asymptote of y = 0
• no x-intercept