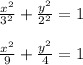Question

NO LINKS! Please help me with this problem

What is the standard form of the equation of the ellipse? ​

Answer 1

`(x^2)/(9)+(y^2)/(4)=1`

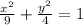
Explanation:

So an ellipse can be expressed in two different but very similar forms:

Horizontal Major Axis:

`((x-h)^2)/(a^2)+((y-k)^2)/(b^2)=1`

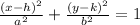
Vertical Major Axis:

`((x-h)^2)/(b^2)+((y-k)^2)/(a^2)=1`

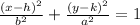
In both equations the length of the major axis is "2a" and the length of the minor axis is "2b"

In the equation you provided, the major axis is horizontal, and the minor axis is vertical.

So looking at the horizontal length, you can see that it's 6, and since this ellipse has a horizontal major axis, that means 2a=6, which means a=3

Looking at the vertical length, you can see that it's 4, and since the ellipse has a vertical minor axis, that means 2b=4, which means b=2

The last thing to note is that the center of an ellipse is (h, k) in the equation, and since here the center is (0, 0) it's (x-0)^2 and (y-0)^2 in the denominator which is just x^2 and y^2

So let's plug in the values into the equation:

`((x-h)^2)/(a^2)+((y-k)^2)/(b^2)=1`

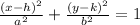
(h, k) = (0, 0)

a = 3

b = 2

`(x^2)/(3^2)+(y^2)/(2^2)=1\\\\(x^2)/(9)+(y^2)/(4)=1`

Answer 2

Here we go ~

The given figure is of a horizontal ellipse with :

• Length of major axis = 2a = 6

so, a = 3

• Length of minor axis = 2b = 4

hence, b = 2

And as it's shown in the figure, the ellipse has its centre at origin, so we can write it's equation as :

`\qquad \sf  \dashrightarrow \: \cfrac{ {x}^(2) }{ {a}^(2) } + \cfrac{ {y}^(2) }{b {}^(2) } = 1`

[ now, plug in the values ]

`\qquad \sf  \dashrightarrow \: \cfrac{ {x}^(2) }{ {3}^(2) } + \cfrac{ {y}^(2) }{2 {}^(2) } = 1`

`\qquad \sf  \dashrightarrow \: \cfrac{ {x}^(2) }{ {9}^{} } + \cfrac{ {y}^(2) }{4 {}^{} } = 1`

That's all, ask me if you have any questions ~