Question

Which of the following is not irrational? (a) (2-√3)2 (b)(√2+√3)2 (c) (√2-√3)(√2+√3) (d)27√7​

Answer 1

Answer: (c)

(√2-√3)(√2+√3)

Explanation:

An irrational number is one that cannot be expressed as the ratio of two integers. In other words it cannot be expressed as
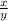`(x)/(y)` where x and y are integers

`√(2)` is irrational

`√(3)` is irrational

In fact the square root of any prime number is irrational. So
`√(5)`,
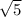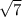`√(7)` etc are irrational. But
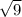`√(9)` is not irrational since it evaluates to 3 which can be expressed as
`(3)/(1)`

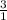
Any expression that contains the square root of a prime number is also irrational

Looking at the choices we see that choices (a), (b) and (d) all evaluate to expressions containing square roots of primes

(a) (2-√3)2 = 4 - 2√3 . Hence irrational

(b) √2+√3)2 = 2√2+2√3. Hence irrational

(d) 27√7​ is irrational

Let's look at choice (c)

(√2-√3)(√2+√3)

An expression
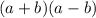`(a+b)(a-b)` can be evaluated as
`a^(2) - b^(2)`

Here a = √2,
`a^(2)` =
`a = √(2)\\ a^2 = (√(2) )^2 = 2\\\\b = √(3) \\b^2 = (√(3) )^2 = 3\\\\a^2 - b^2 = 2-3 = -1\\`

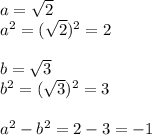
This is a whole number(integer) and all integers are rational numbers

Hence correct answer is (c)