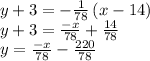Question

Find an equation of the line perpendicular to y = − 7 8 x + 2 and containing the point (14, − 3)

Answer 1

`y=(-x)/(78) -(220)/(78)`

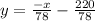
Explanation:

Remember to create a line perpendicular to one another the slope has to be the reverse reciprocal of the first line.

Given the current slope is
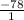`(-78)/(1)` the new slope would be
`(1)/(78)`.

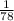To find the line that passes through a point with a given slope we must use point slope form, remember the default equation of point slope form:

`y-y1=m(x-x1)`

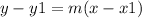
Where y1 is the y value of the point, m is the slope, and x1 is the x value of the point.

Lets substitute in our values

`y-(-3)=(-1)/(78) (x-14)`

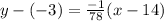
Simplify the equation

`y+3=-(1)/(78)\left(x-14\right)\\y+3=(-x)/(78)+(14)/(78)\\y=(-x)/(78)-(220)/(78)\\`