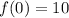Question

Please help me!

A scientist is comparing the bacteria population on two surfaces t days after it is cleaned with bleach.

Bacteria on the kitchen counter is initially measured at 5 and doubles every 3 days.

Bacteria on the stove is initially measured at 10 and doubles every 4 days.

1. After how many days will the bacteria population on both surfaces be equal?
2. What is the bacteria population when both surfaces have an equal population?

Answer 1

They are only equal on day 0, both having 10 population.

Explanation:

Given the bacteria on the counter is initially measured at 5 and doubles every 3 days we can generate the following geometric equation:

`f(x)=10*2^{(x)/(3) }`

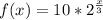
Given the bacteria on the stove is measured at 10 and doubles every 4 days we can create another equation:

`f(x)=10*2^{(x)/(4) }`

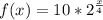
To find how many days it will take for the bacteria population to equal the same lets set both equations equal to eachother:

`10*2^(x/3)=10*2^(x/4)`

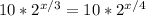
Divide both sides by 10

`2^(x/3)=2^(x/4)`

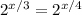
Since both exponents have the same base we can set the exponents equal to eachother and solve for x:

`(x)/(3)=(x)/(4)`

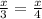
Multiply both sides by 3 to isolate x on the left side

`x=(3x)/(4)`

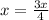
Multiply both sides by 4 to remove fraction

`4x=3x`

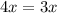
Subtract 3x to isolate x on the left side

`x=0`

Plug x into one of our original equations

`f(0)=10*2^(0/3)`

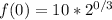
Solve

`f(0)=10`