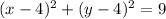Question

What is the general form of the equation for the given circle?

Answer 1

Circle Equations

The general equation for a circle is
`(x-h)^2+(y-k)^2=r^2`, where
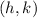`(h,k)` is the centre of the circle and
`r` is the radius.

Solving the Question

First, we can determine the centre of the circle.

( _ , _ )

The point directly on top is (4,7). Because it lies on the same vertical line as the centre, they have the same x-coordinate.

(4, _ )

The point directly to the right of it is (7,4). Because it lies on the same horizontal line as the centre, they have the same y-coordinate.

(4,4)

Therefore, the centre of the circle is (4,4). Plug this into the general equation:

`(x-h)^2+(y-k)^2=r^2\\(x-4)^2+(y-4)^2=r^2`

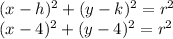
Now, we can determine the radius of the circle.

To do this, we can calculate the distance between the centre of the circle and one of the given points that lie on the circumference.

The centre is (4,4), and one of the points is (4,7). Because they only have a difference of 3 units in the y-direction (and none in the x-direction), this means that the radius is 3 units. Plug this into the general equation:

`(x-4)^2+(y-4)^2=r^2\\(x-4)^2+(y-4)^2=3^2\\(x-4)^2+(y-4)^2=9`

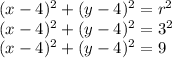
Answer

`(x-4)^2+(y-4)^2=9`