Question 1:
1) Given - It is given in the problem
2) Corresponding Angles Postulate - If a transversal (line l) intersects two parallel lines (line h and line g), then the corresponding angles must be equal.
3) Transitive Property of Congruence - Since it's given that
 and we showed in line 2 that
and we showed in line 2 that
 , it should be true that
, it should be true that

4) Converse of Corresponding Angles Postulate - If a transversal (line g) intersects two lines (lines l and m), and the corresponding angles that form have equal measure, then the lines are parallel.
Question 2:
1) Given - It is given in the problem
2) Definition of Angle Bisector - It's given that
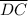 bisects
bisects
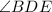 , which means that
, which means that
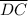 is the angle bisector, and the angle is divided into two angles of the same measure.
is the angle bisector, and the angle is divided into two angles of the same measure.
3) Transitive Property of Congruence - Since we showed in line 2 that
 and its given that
and its given that
 , it should be true that
, it should be true that

4) Converse of the Alternate Interior Angles Theorem - If a transversal (
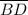 ) intersects two lines (
) intersects two lines (
 and
and
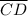 ) and the alternate interior angles formed have the same measure, then the lines are parallel.
) and the alternate interior angles formed have the same measure, then the lines are parallel.