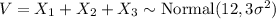The sum of normally distributed random variables is also a normally distributed random variable.
Given
 random variables with
random variables with
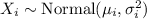 , their sum is
, their sum is
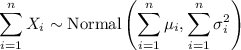
i.e. normally distributed with mean and variance equal to the sums of the means and variances of the
 .
.
In this case, each of
 are normally distributed with
are normally distributed with
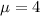 and
and
 = ... I'm not sure what you meant for the variance, so I'll keep it symbolic. Then
= ... I'm not sure what you meant for the variance, so I'll keep it symbolic. Then