Answer:
- rule: an = 10010 -250(n -1)
- day 14: 6760 words
Explanation:
The first three terms of the arithmetic sequence for the number of words written are 10010, 9760, 9510. These have a common difference of 9760-10010 = -250. The first term and common difference can be used to make the explicit equation for the words written on the n-th day.
Formula for Arithmetic Sequence
The explicit formula for the n-th term of an arithmetic sequence with first term a₁ and common difference d is ...
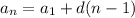
Application
For first term a₁ = 10010 and common difference d = -250, the explicit rule is ...
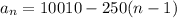
On day 14, n=14, and the number of words written is ...
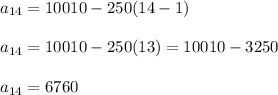
The writer would write 6760 words on the 14th day.