As you've pointed out, R is a different region that I originally thought. The area of R can be computed using either
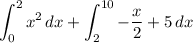
or
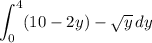
Either way, you've gotten the correct area for part (a).
For part (b), we can use part of the integral with respect to
 above. The horizontal distance between the curves
above. The horizontal distance between the curves
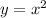 and
and
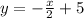 is obtained by first solving for
is obtained by first solving for
 ,
,
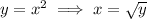
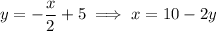
so the length of each cross section is
 .
.
The height of each cross section is
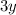 .
.
Then the volume of the solid is
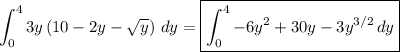
The instructions don't say to evaluate, but if you're looking for practice the volume ends up being 368/5, or 73 3/5.